Kailash Ahirwar, co-founder of machine learning startup Mate Labs, briefly introduced 13 neural network activation functions.
The activation function introduces non-linearity into the network, so the activation function itself is also called nonlinearity. Neural networks are universal function approximators, while deep neural networks are based on backpropagation training and therefore require subtle activation functions. Backpropagation applies a gradient descent on this function to update the weight of the network. Understanding the activation function is very important because it plays a key role in the quality of deep neural networks. This article will list and describe different activation functions.
Linear activation function
The identity or linear activation function is the simplest activation function. The output is proportional to the input. The problem with the linear activation function is that its derivatives are constants, gradients are constants, and gradients do not work.
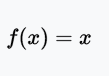
Range: (-∞, +∞)
Example: f(2) = 2 or f(-4) = -4
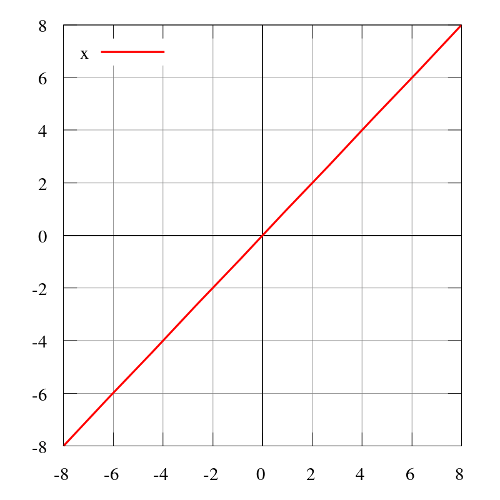
Step function
The step function (Heaviside step function) is usually only useful in single-layer sensors, which are early forms of neural networks and can be used to classify linearly separable data. These functions can be used for binary classification tasks. The output is either A1 (if the sum of the inputs is above a certain threshold) or A0 (if the sum of the inputs is below a certain threshold). The perceptron uses A1 = 1, A0 = 0.
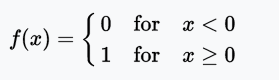
Range: 0 or 1
Examples: f(2) = 1, f(-4) = 0, f(0) = 0, f(1) = 1
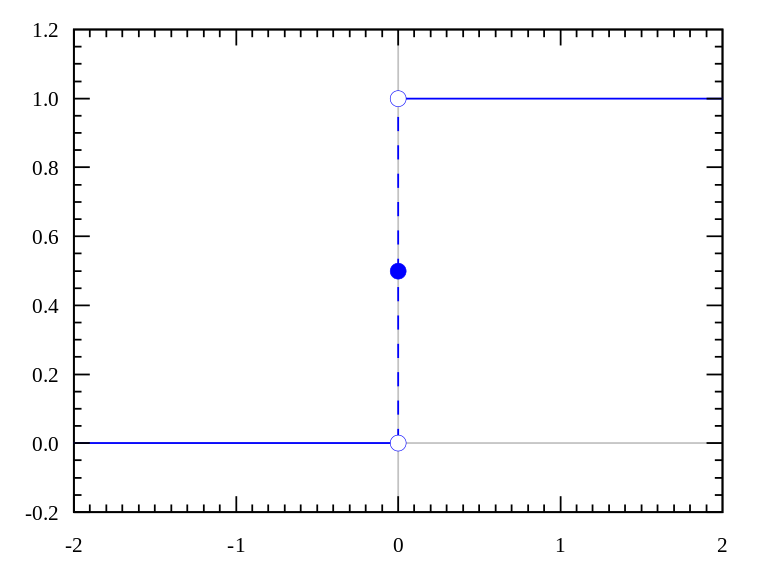
Image source: Wikipedia
Sigmoid function
Sigmoid functions, also known as logistic activation functions, are most often used for binary classification problems. It has the problem of disappearing gradients. After a certain number of epochs, the network refuses to learn, or learns very slowly because the input (X) causes very small changes in the output (Y). The sigmoid function is now mainly used for classification problems. This function is more likely to encounter the saturation of the subsequent layer, resulting in difficult training. Calculating the derivative of a sigmoid function is very simple.
In terms of the back-propagation process of neural networks, each layer (at least) squeezes in a quarter of the error. Therefore, the deeper the network, the more knowledge about data will be "lost." The "larger" error of some output layers may not affect the synaptic weights of the neurons in the relatively shallow layer ("lighter" means close to the input layer).
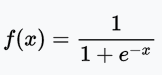
Sigmoid function definition
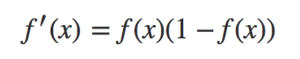
Derivatives of the sigmoid function
Range: (0, 1)
Examples: f(4) = 0.982, f(-3) = 0.0474, f(-5) = 0.0067
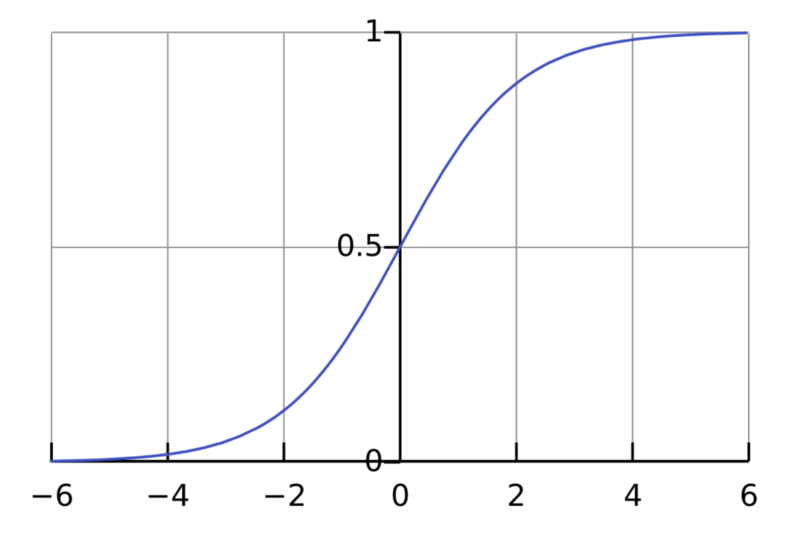
Image source: Wikipedia

Image credit: deep learning nano foundation
Tanh function
The tanh function is a stretched sigmoid function centered at zero, so the derivative is steeper. Tanh converges faster than the sigmoid activation function.
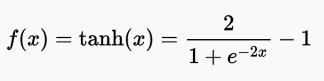
Range: (-1, 1)
Example: tanh(2) = 0.9640, tanh(-0.567) = -0.5131, tanh(0) = 0
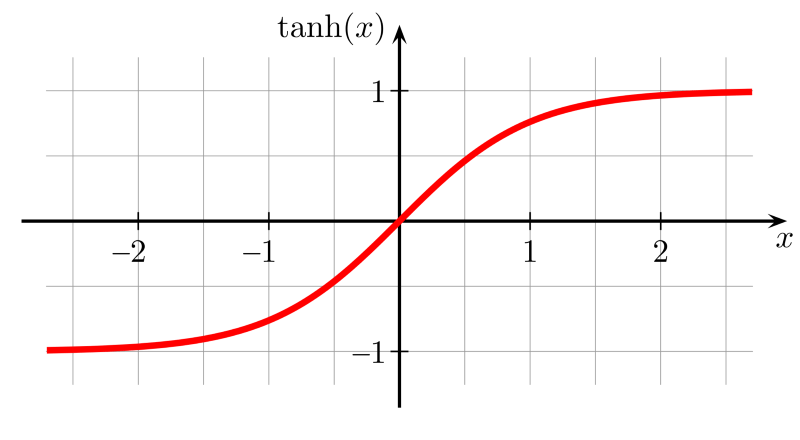
Image source: Wikipedia
ReLU function
The ReLU (Rectified Linear Unit) training speed is six times faster than tanh. When the input value is less than zero, the output value is zero. When the input value is greater than or equal to zero, the output value is equal to the input value. When the input value is positive, the derivative is 1, so the sigmoid function does not exhibit the squeezing effect when backpropagating.
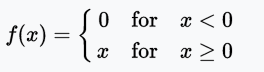
Range: [0, x)
Example: f(-5) = 0, f(0) = 0, f(5) = 5

Image source: Wikipedia
Unfortunately, ReLU may be very fragile during training and may be "dead." For example, a larger gradient through a ReLU neuron may cause the weights to update too far, causing the neurons to no longer be activated by any data point. If this happens, the gradient through this cell will never be zero thereafter. That is, ReLU units may irreversibly die during training because they are kicked out of the data stream. For example, you may find that if the learning rate is set too high, 40% of the networks may be "dead" (ie neurons will never be active on the entire training dataset). Setting a suitable learning rate can alleviate this problem.
-- Andrej Karpathy CS231n Course
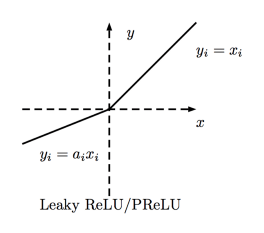
Leaky ReLU function
Leaky ReLU allows a small non-zero gradient when the cell is inactive. Here, the small non-zero gradient is 0.01.
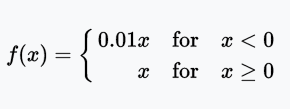
Range: (-∞, +∞)
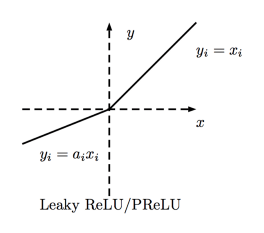
PReLU function
The PReLU (Parametric Rectified Linear Unit) function is similar to Leaky ReLU, except that the coefficients (small non-zero gradients) are used as parameters for the activation function. This parameter, like other network parameters, is learned during training.
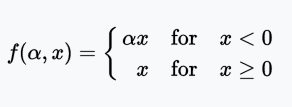
Range: (-∞, +∞)
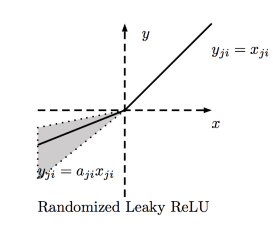
RReLU function
RReLU is also similar to Leaky ReLU, except that the coefficients (small non-zero gradients) take a random range of values ​​during training and are fixed during testing.
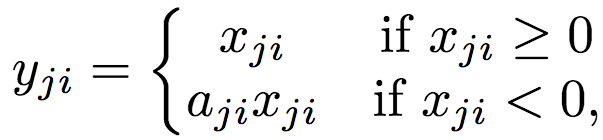
Range: (-∞, +∞)
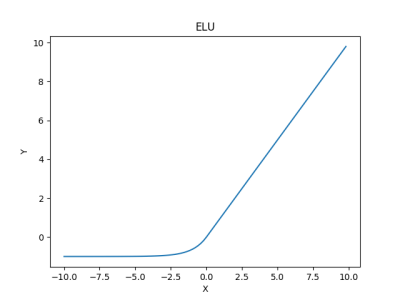
ELU function
The ELU (Exponential Linear Unit) tries to speed up learning. Based on the ELU, it is possible to obtain higher classification accuracy than ReLU. Here α is a hyper-parameter (limit: α ≥ 0).
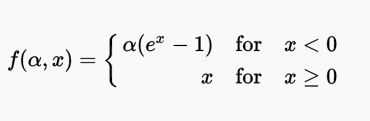
Range: (-α, +∞)
SELU function
SELU (Scaled Exponential Linear Unit) is a stretched version of the ELU.
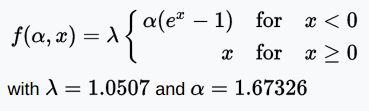
Image credit: Elior Cohen
SReLU function
The SReLU (S-shaped Rectified Linear Activation Unit) consists of three piecewise linear functions. The coefficient as a parameter will be learned in network training.
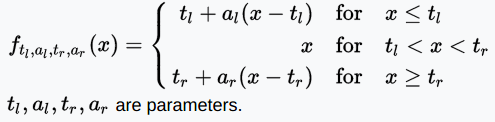
Range: (-∞, +∞)
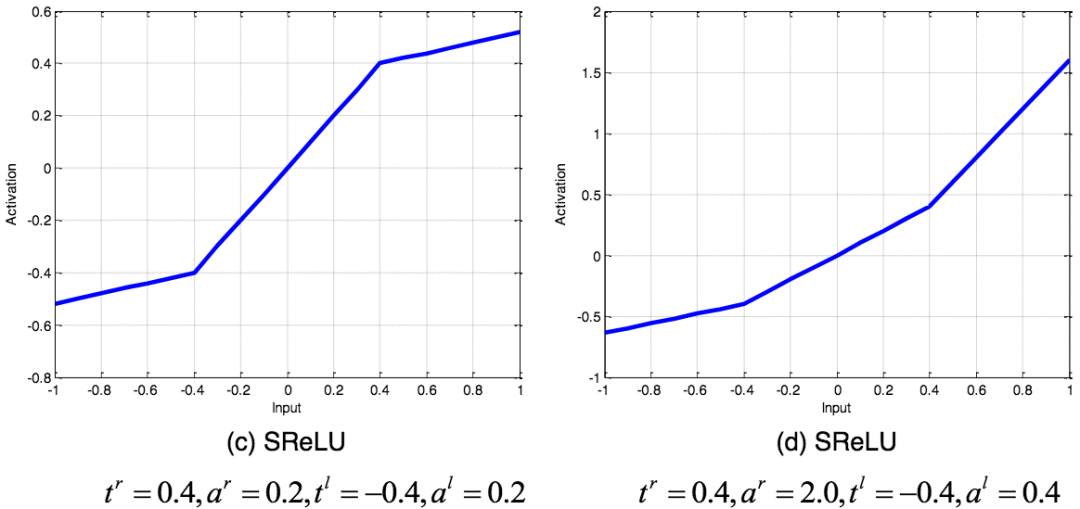
SReLU images with different parameters; picture source: arXiv: 1512.07030
APL function
APL (Adaptive Piecewise Linear) function
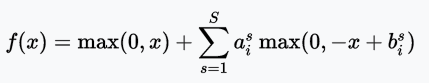
Picture source: arXiv: 1512.07030
Range: (-∞, +∞)

SoftPlus function
The derivative of the SoftPlus function is a logistic function. In general, ReLU and SoftPlus are similar, except that SoftPlus is smooth and subtly close to zero. In addition, calculating ReLU and its derivatives is much easier than SoftPlus.
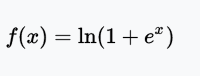
Range: (0, ∞)
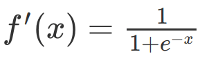
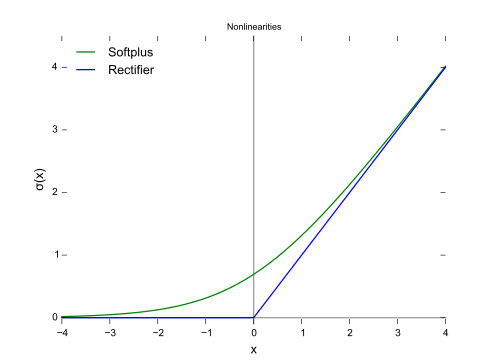
Image source: Wikipedia
Bent identity function
The bent identity function, as the name implies, bends the identity function.
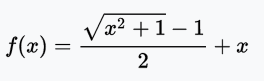
Range: (-∞, +∞)
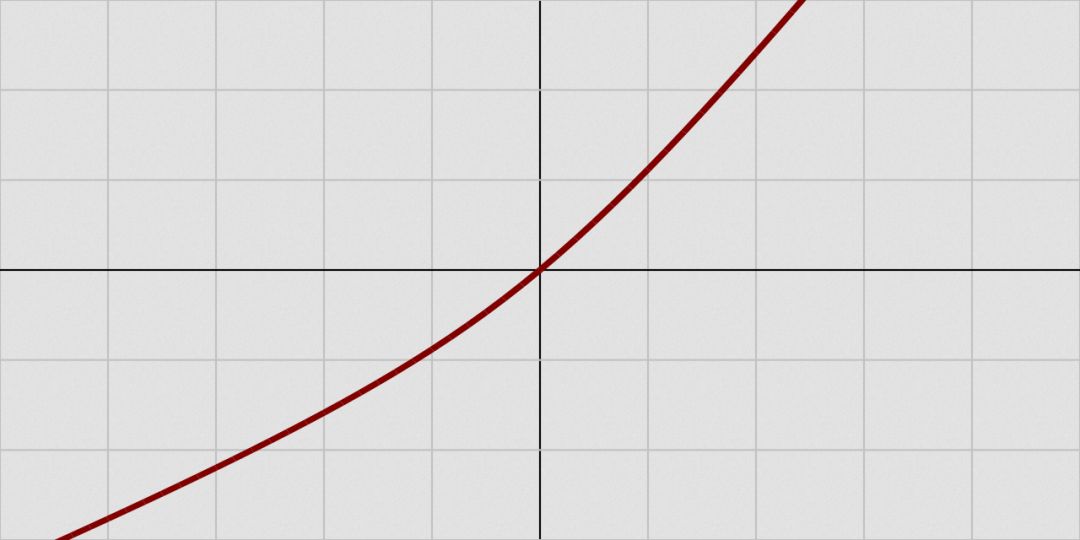
Image source: Wikipedia
Softmax function
The softmax function converts the original value to a posterior distribution that can be used to measure certainty. Like sigmoid, softmax squeezes the output value of each cell between 0 and 1. However, softmax also ensures that the sum of the output is equal to 1.
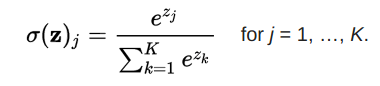
Image credit: dataaspirant.com
The output of the softmax function is equivalent to the category probability distribution, which tells you the probability that any classification is true.
Conclusion
When selecting an activation function, ReLU and its variants are preferred over sigmoid or tanh. At the same time ReLU and its variants train faster. If ReLU causes neuronal death, use Leaky ReLU or other variants of ReLU. Sigmoid and tanh are bothered by the disappearance of the gradient problem and should not be used in hidden layers. It is better to use ReLU and its variants in the hidden layer. Use activation functions that are easy to find and train.
We provide many kinds of Polymeric Diaphragm to meet the different needs of different customers, they are widely used in Hi-Fi speakers,professional audio,horn speakers,car speakers and other high-end products.
We are experienced in manufacturing and have strong capability.
Our products are popular in many countries and areas.
We have professional acoustical testing systems and instruments.
We promise to offer you highest quality and best service!
Polymeric Diaphragm,Voice Coil Diaphragm,Diaphragm Voice Coil For Horn Driver,Voice Coil Phenolic Diaphragm
Taixing Minsheng Electronic Co.,Ltd. , https://www.ms-speakers.com
