The following are the top 9 algorithm-related concepts in a programming interview. I will illustrate these concepts with some simple examples. Since it takes more effort to fully grasp these concepts, this list is only an introduction. This article will look at the problem from a Java perspective, including the following concepts:
String
2. Linked list
3. Tree
Figure
5. Sorting
6. Recursive vs. iteration
7. Dynamic planning
8. Bit operation
9. Probability issues
String
If the IDE does not have code auto-completion, you should keep the following in mind.
toCharArray()// Get the char array corresponding to the string
Arrays.sort() // Array sorting
Arrays.toString(char[]a)// Array into a string
charAt(intx)// Get the character at an index
Length()// string length
Length / / array size
2. Linked list
In Java, the implementation of a linked list is very simple. Each node Node has a value val and a link next to the next node.
classNode{
Intval;
Node next;
Node(intx){
Val = x;
Next = null;
}
}
Two well-known applications for linked lists are Stack Stack and Queue Queue.
Stack:
classStack{
Node top;
publicNode peek(){
If(top != null){
Returntop;
}
Returnnull;
}
publicNode pop(){
If(top == null){
Returnnull;
}else{
Node temp = newNode(top.val);
Top = top.next;
Returntemp;
}
}
Publicvoidpush(Noden){
If(n != null){
N.next = top;
Top = n;
}
}
}
queue:
classQueue{
Node first, last;
Publicvoidenqueue(Noden){
If(first == null){
First = n;
Last = first;
}else{
Last.next = n;
Last = n;
}
}
publicNode dequeue(){
If(first == null){
Returnnull;
}else{
Node temp = newNode(first.val);
First = first.next;
If(last == temp)last = first;
Returntemp;
}
}
}
3. Tree
The tree here usually refers to a binary tree, and each node contains a left child node and a right child node, like this:
classTreeNode{
Intvalue;
TreeNode left;
TreeNode right;
}
Here are some concepts related to trees:
Balance vs. Unbalance: In a balanced binary tree, the depths of the left and right subtrees of each node differ by at most 1 (1 or 0).
Full Binary Tree: There are two children for each node except the leaf node.
Perfect Binary Tree: A full binary tree with the following properties: all leaf nodes have the same depth or are at the same level, and each parent node must have two children.
Complete Binary Tree: In a binary tree, except for the last one, each layer is completely filled, and all nodes must be left as far as possible.
Translator's Note: The perfect binary tree is also vaguely called the complete binary tree. An example of a perfect binary tree is an ancestor diagram of a person at a given depth, because each person must have two birth parents. A fully binary tree can be thought of as a perfect binary tree with a number of extra left-left leaf nodes. Question: What is the difference between a perfect binary tree and a full binary tree?
Figure
The graph related questions mainly focus on depth first search and bread first search.
Below is a simple implementation of the breadth-first search.
1) Define GraphNode
classGraphNode{
Intval;
GraphNode next;
GraphNode[]neighbors;
Booleanvisited;
GraphNode(intx){
Val = x;
}
GraphNode(intx,GraphNode[]n){
Val = x;
Neighbors n n;
}
publicStringtoString(){
Return"value: "+ this.val;
}
}
2) Define a queue Queue
classQueue{
GraphNode first, last;
Publicvoidenqueue(GraphNoden){
If(first == null){
First = n;
Last = first;
}else{
Last.next = n;
Last = n;
}
}
publicGraphNode dequeue(){
If(first == null){
Returnnull;
}else{
GraphNode temp = newGraphNode(first.val,first.neighbors);
First = first.next;
Returntemp;
}
}
}
3) Width-first search using queue Queue
publicclassGraphTest{
Publicstaticvoidmain(String[]args){
GraphNode n1 = newGraphNode(1);
GraphNode n2 = newGraphNode(2);
GraphNode n3 = newGraphNode(3);
GraphNode n4 = newGraphNode(4);
GraphNode n5 = newGraphNode(5);
N1.neighbors = newGraphNode[]{n2,n3,n5};
N2.neighbors = newGraphNode[]{n1,n4};
N3.neighbors = newGraphNode[]{n1,n4,n5};
N4.neighbors = newGraphNode[]{n2,n3,n5};
N5.neighbors = newGraphNode[]{n1,n3,n4};
breathFirstSearch(n1,5);
}
publicstaticvoidbreathFirstSearch(GraphNode root,intx){
If(root.val == x)
System.out.println("find in root");
Queue queue = newQueue();
Root.visited = true;
Queue.enqueue(root);
While(queue.first != null){
GraphNodec = (GraphNode)queue.dequeue();
For(GraphNoden: c.neighbors){
If(!n.visited){
System.out.print(n + " ");
N.visited = true;
If(n.val == x)
System.out.println("Find "+n);
Queue.enqueue(n);
}
}
}
}
}
5. Sorting
The following is the time complexity of different sorting algorithms. You can go to the wiki to see the basic ideas of these algorithms.
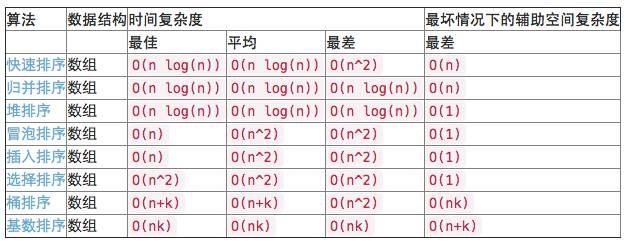
6. Recursive vs. iteration
For programmers, recursion should be an in-built thought, which can be illustrated by a simple example.
Question: There are n steps, only one step or two steps at a time, how many ways to go.
Step 1: Find the relationship between the first n steps and the first n-1 steps.
In order to complete the n steps, there are only two methods: one step from n-1 steps to climb or two steps from n-2 steps. If f(n) is the number of methods that climb to the nth step, then f(n) = f(n-1) + f(n-2).
f(0) = 0; f(1) = 1;
Step 2: Make sure the start condition is correct.
Publicstaticintf(intn){
If(n <= 2)returnn;
Intx = f(n-1) + f(n-2);
Returnx;
}
The time complexity of the recursive method is exponential for n because there are many redundant calculations, as follows:
f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
The immediate idea is to convert recursion into iterations:
Publicstaticintf(intn){
If(n <= 2){
Returnn;
}
Intfirst = 1, second = 2;
Intthird = 0;
For(inti = 3;i <= n;i++){
Third = first + second;
First = second;
Second = third;
}
Returnthird;
}
7. Dynamic planning
Dynamic programming is a technique for solving the following types of problems:
A problem can be solved by solving the problem of the smaller sub-problem (Translator's Note: the optimal solution of the problem contains the optimal solution of its sub-problem, that is, the optimal sub-structure property).
The solution to some subproblems may need to be calculated multiple times (Translator's Note: that is, the overlapping nature of subproblems).
The solution to the sub-question is stored in a table so that each sub-question is only counted once.
Need extra space to save time.
The problem of climbing stairs is in full compliance with the above four properties, so it can be solved by dynamic programming.
Publicstaticint[]A = newint[100];
Publicstaticintf3(intn){
If(n <= 2)
A[n]= n;
If(A[n] > 0)
returnA[n];
Else
A[n] = f3(n-1) + f3(n-2);//store results so only calculate once!
returnA[n];
}
8. Bit operation
Bit operator:
| or | versus | Or | Shift left | Shift right | non- |
| 1|0=1 | 1&0=0 | 1^0=1 | 0010<<2=1000 | 1100>>2=0011 | ~1=0 |
Get the ith bit of the given number n: (i counts from 0 and starts from the right)
publicstaticbooleangetBit(intnum,inti){
Intresult = num & (1< If(result == 0){ Returnfalse; }else{ Returntrue; } For example, get the second digit of the number 10: i=1, n=101<<1= 101010&10=1010 is not 0, so return true; 9. Probability issues Solving probabilistic related problems usually requires a good planning of the problem. There is just one simple example of such a problem: There are 50 people in a room, so what is the probability that at least two people will have the same birthday? (Ignore the fact of the leap year, which is 365 days a year) The probability of calculating certain things can often be converted to calculate their opposite faces first. In this example, we can calculate the probability that everyone's birthdays will be different from each other, namely: 365/365 * 364/365 * 363/365 * ... * (365-49)/365, so at least two birthdays The same probability is 1 – this value. PublicstaticdoublecaculateProbability(intn){ Doublex = 1; For(inti=0;i x *= (365.0-i)/365.0; } Doublepro = Math.round((1-x) * 100); Returnpro/100; } calculateProbability(50) = 0.97 Vape Pen Disposable E Cigarette,Disposable Vape Pen Stick,Disposable Vape Puff Bar,Electronic Cigarette Vape Puff Bar Shenzhen Kate Technology Co., Ltd. , https://www.katevape.com
